|
Консультант по электроснабжению
Не нашли нужный онлайн-расчет по электроэнергетике? Свяжитесь с нами!
Бот Яша
Бот Яша подскажет как найти нужный онлайн расчет или базу данных на сайте "Онлайн Электрик".
Написать боту.
Research results of impedance of power line in case of three-phase short circuitS.Y. LyubomirovTechnical College - Smolyan branch Plovdiv University "Paisii Hilendarski" In recent years, power systems and medium voltage distribution networks grow rapidly and their operation requires more and more new information systems. Key words: Determination of the distance to the fault, distribution networks of medium voltage, parameters of transmission lines, impedance.
Въведение През последните години се наблюдава стремеж към постигане на по-високо качество от гледна точка на доставки и услуги, което е предпоставка за внедряването и използването на повече компютъризация, автоматизация и контролно измервателни устройства в електроенергийната система. Друг важен аспект е конкурентоспособността на електрическите пазарни мощности и нарастващата взискателност към електрическите компании, да запазят търсенето и да повишат показателите на качеството на енергията в рамките на изискваните стандарти. Това води до насърчаването на развитието и внедряването на нови техники, необходими за повишаване на надеждност, селективност, чувствителност и бързодействие в разпределителните мрежи. В този контекст, бързото и ефективно определяне на мястото на повредата в тези мрежи е един от начините за подобряване на тези показатели. По този начин, различни технически подходи при определяне на разстоянието до мястото на повредата са предложени и представят резултати, които показват необходимостта от нови инвестиции проучвания, свързани с тази проблематика. Късите съединения са най-честото смущаващо въздействие в тези системи и информацията за техния вид и място е особено важна за отстраняването им и постигане на надеждно електрозахранване на потребителите. Задачата няма радикално решение поради факта, че разпределителните мрежи са силно разклонени и едно измерено разстояние отговаря на няколко места в тях. Нова пречка е и непрекъснатото въвеждане на нови алтернативни източници на енергия, които често се включват към електропроводите средно напрежение и ги превръща в електропроводи, захранвани от две страни.
1. Таблично и графично представяне на резултатите от трифазно късо съединение на единичен въздушен електропровод В приложението са дадени зависимостите на импеданса, активното съпротивление и раектанса при трифазно късо съединение с различна стойност на преходно съпротивление в мястото на повредата при въздушен електропровод захранен от едната страна. Графично представените резултати от трифазното късо съединение са направени с програмния продукт Matlab R2010b и таблично онагледени в Microsoft Excel. Данните за електропровода са следните: Сечение АС95; Дължина 11.3 km; R0=0.33 ohm/km; X0=0.367 ohm/km. Импедансът на линията Zline е равен на = 3.7290 + 4.1471i. Таблица 1. Изчисление за трифазно късо съединение без преходно съпротивление в мястото на повредата.
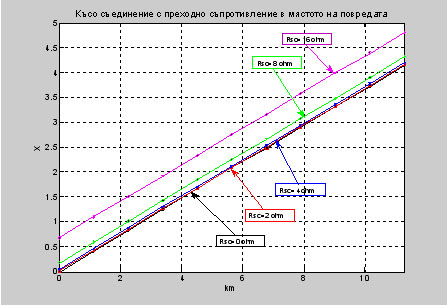
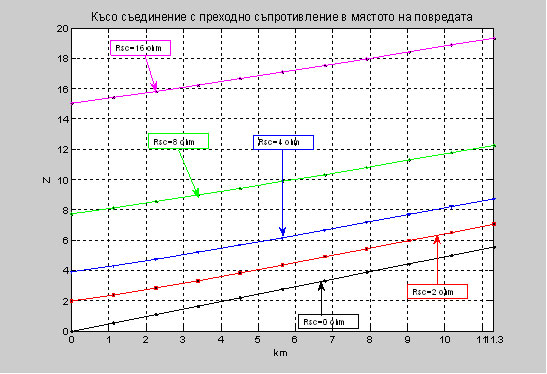
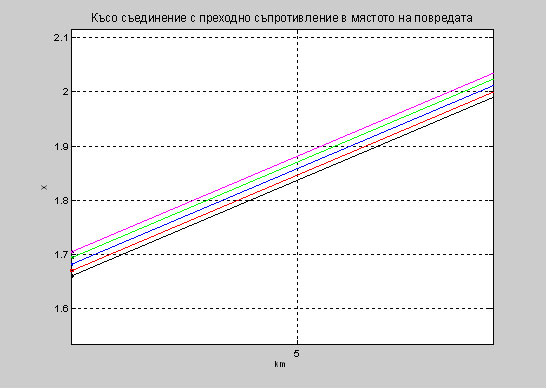
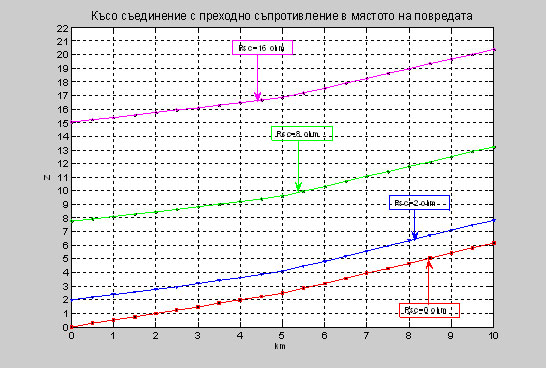
От таблично представените резултати се забелязва, че когато няма преходно съпротивление в мястото на повредата, то изчисления импеданс отговаря на точното местоположение на повредата. Фиг .1. Графично представяне на X в зависимост от дължината на електропровода при стойностти за активното съпротивление Rsc=0, 2, 4, 8, 16 ohm. Фиг. 2. Графично представяне на импеданса Z в зависимост от дължината на електропровода при стойностти за активното съпротивление Rsc=0, 2, 4, 8, 16 ohm.
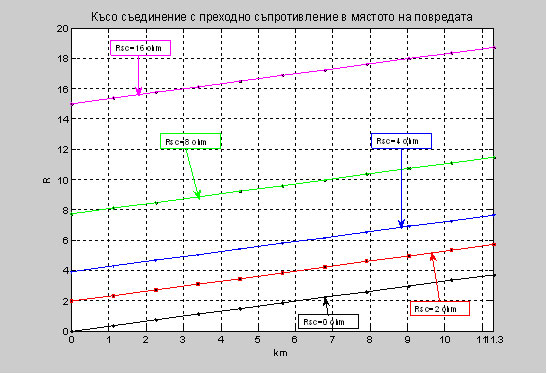
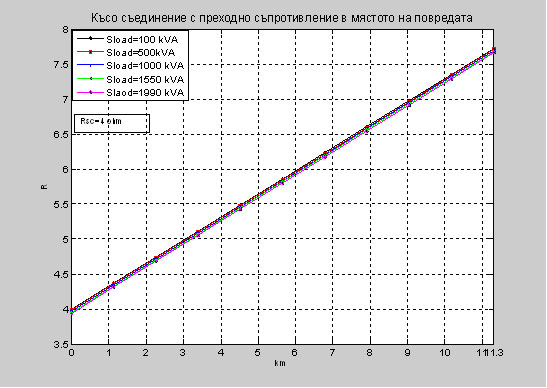
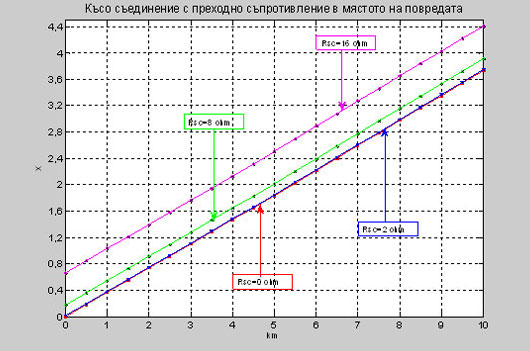
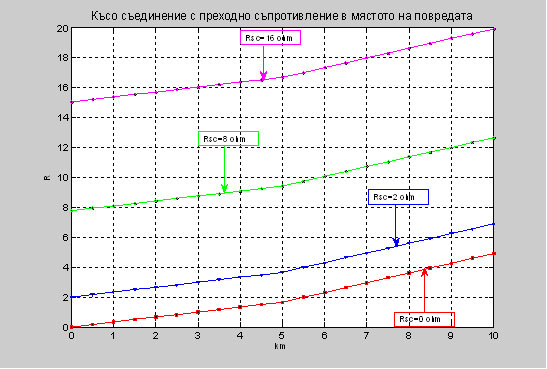
Фиг. 3. Графично представяне на R в зависимост от дължината на електропровода при стойностти за активното съпротивление Rsc=0, 2, 4, 8, 16 ohm. Фиг. 4. Графично представяне на R в зависимост от промяната на товара при стойност за активното съпротивление Rsc=4 ohm. Фиг. 5. Графично представяне на Х в зависимост от промяната на товара при стойност за активното съпротивление Rsc=4 ohm. 2. Таблично и графично представяне на резултатите от трифазно късо съединение на два последователно свързани въздушни електропровода В приложението са дадени зависимостите на импеданса, активното съпротивление и раектанса при трифазно късо съединение с различна стойност на преходно съпротивление в мястото на повредата при два последователно свързани въздушни електропроводи с различни сечения захранени от едната страна. Графично представените резултати от трифазното късо съединение са направени с програмния продукт Matlab R2010b и таблично онагледени в Microsoft Excel. Данните за електропровода са следните: • първия електропровод P е със сечение АС95, дължина 5 km, R0=0.33 ohm/km, X0=0.367 ohm/km; • втория електропровод R е със сечение АС50, дължина 5 km, R0=0.65 ohm/km, X0=0.3800 ohm/km. Таблица 2. Изчисление за трифазно късо съединение без преходно съпротивление в мястото на повредата при два електропровода с различни параметри.
При изчисленията за товара Zload=1990000 VA, cosφ=0,8. Получената стойност за импеданса на първия електропровод е Zp1 =1.65+1.835i оhm. Получената стойност за втория електропровод е Zr1 =3.25+1.9i оhm. Графиките са правени при изчисления на база само импеданси. Фиг. 6. Графично представяне на импедансите Z в зависимост от дължината на електропровода при стойностти за активното съпротивление Rsc=0, 2, 8, 16 ohm. Фиг. 7. Графично представяне на раектанса X в зависимост от електропроводите при стойностти за активното съпротивление Rsc=0, 2, 8, 16 ohm.
Фиг. 8. Графично представяне на X в зависимост от дължината на електропровода при стойностти за активното съпротивление Rsc=0, 2, 8, 16 ohm.
3. Влияние на товара при изчисляване на импеданса на далекопровод при трифазно късо съединение В приложението са дадени зависимостите на импеданса, активното съпротивление и раектанса при трифазно късо съединение с различна стойност на преходно съпротивление в мястото на повредата при два последователно свързани въздушни електропроводи с различни сечения захранени от едната страна. Графично представените резултати от трифазното късо съединение са направени с програмния продукт Matlab R2010b и таблично онагледени в Microsoft Excel.
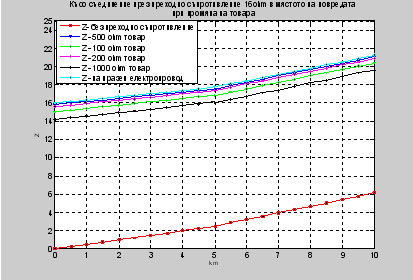
Фиг. 9. Показани са графично резултатите за Z при късо съединение през преходно съпро-тивление 16 Ohm , при промяна на товара, при празен ход на електропроводите и без преходно съпротивле-ние.
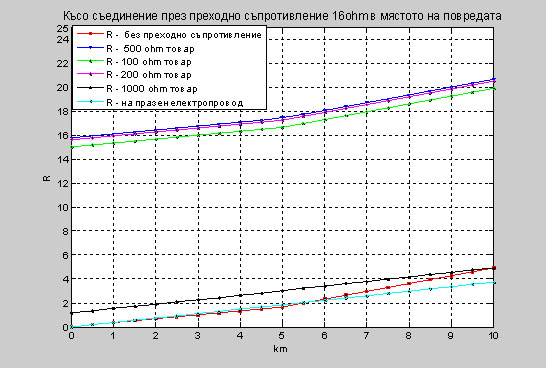
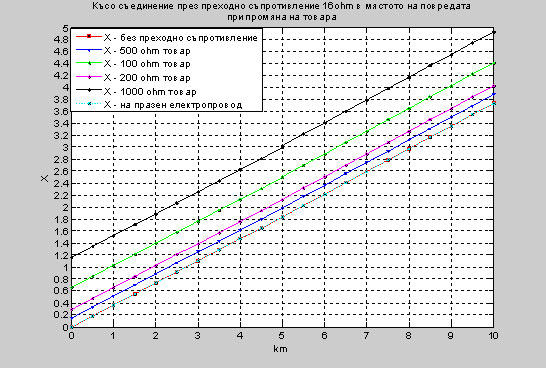
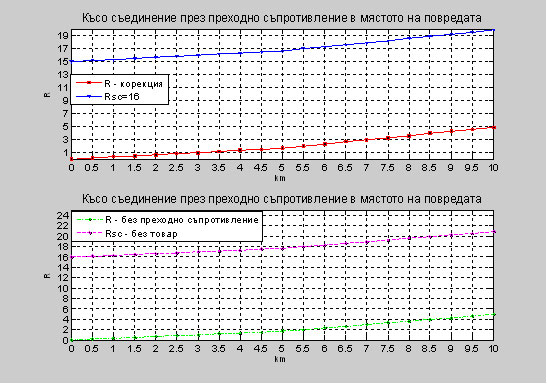
Фиг. 10. Показани са графично резултатите за R при късо съединение през преходно съпротивление 16 Ohm , при промяна на товара, при празен ход на електропроводите и без преходно съпротивление. Фиг. 11. Показани са графично резултатите за X при късо съединение през преходно съпротивление 16 Ohm, при промяна на товара, при празен ход на електропроводите и без преходно съпротивление. Таблица 3. Изчисление за трифазно късо съединение с преходно съпротивление Rsc1=16 ohm в мястото на повредата при два електропровода с различни параметри и товар Sload=200 ohm.
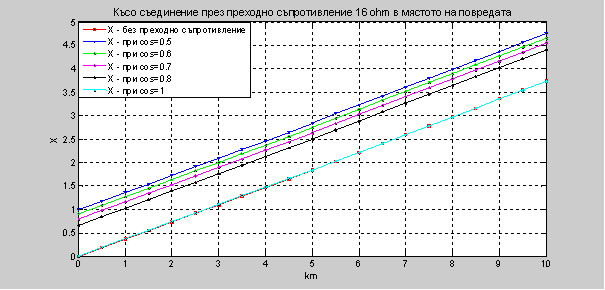
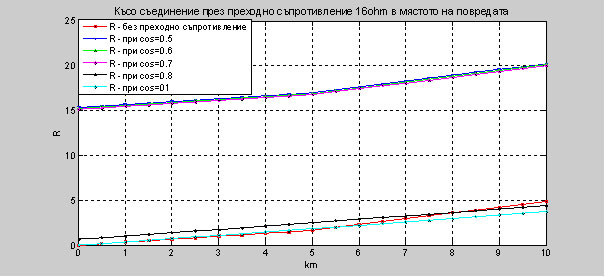
4. Изследване на импеданса на далекопровод при трифазно късо съединение при промяна на cos φ (от 0.5 ÷ 1) В приложението са дадени зависимостите на импеданса, активното съпротивление и раектанса при трифазно късо съединение с Rsc1=16 ohm преходно съпротивление и промяна на cos φ (от 0.5 ÷ 1). При два последователно свързани въздушни електропроводи с различни сечения захранени от едната страна, с дължини на електропроводите 5 km. Графично представените резултати от трифазното късо съединение са направени с програмния продукт Matlab R2010b и таблично онагледени в Microsoft Excel. Фиг 12. Показани са графично резултатите за X при късо съединение през преходно съпротивление 16 Ohm , при промяна на cos φ (от 0.5 ÷ 1) и без преходно съпротивление.
Фиг. 13. Показани са графично резултатите за R при късо съединение през преходно съпротивление 16 Ohm , при промяна на cos φ (от 0.5 ÷ 1) и без преходно съпротивление.
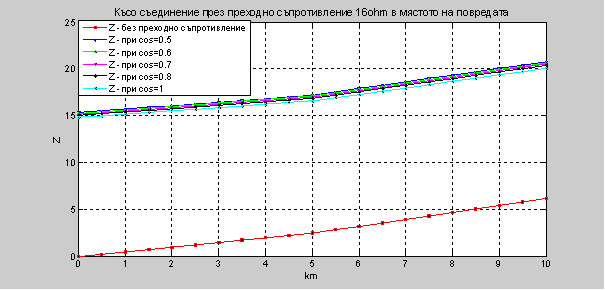
Фиг. 14. Показани са графично резултатите за Z при късо съединение през преходно съпротивление 16 Ohm , при промяна на cos φ (от 0.5 ÷ 1) и без преходно съпротивление.
Таблица 4. Изчисление за трифазно късо съединение с преходно съпротивление Rsc1=16 ohm в мястото на повредата при Rsc1=16 ohm преходно съпротивление и промяна на cos φ (от 0.5 ÷ 1), разделена на две части.
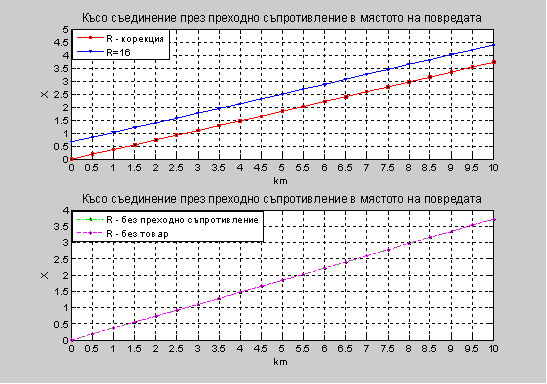
5. Изследване на импеданса на далекопровод при трифазно късо съединение при отчитане влиянието на активното съпротивление и корекция В приложението са дадени зависимостите на импеданса, активното съпротивление и раектанса при трифазно късо съединение с различна стойност на преходно съпротивление в мястото на повредата при два последователно свързани въздушни електропроводи с различни сечения захранени от едната страна. Графично представените резултати от трифазното късо съединение са направени с програмния продукт Matlab R2010b и таблично онагледени в Microsoft Excel. Фиг. 15. Показани са графично резултатите за X при късо съединение през преходно съпротивление 16 Ohm , при корекция на 16 Ohm, при празен ход на електропроводите и без товар. Фиг. 16. Показани са графично резултатите за Z при късо съединение през преходно съпротивление 16 Ohm , при корекция на 16 Ohm, при празен ход на електропроводите и без товар. Фиг. 17. Показани са графично резултатите за R при късо съединение през преходно съпротивление 16 Ohm , при корекция на 16 Ohm, при празен ход на електропроводите и без товар. Заключение От наблюдаването на показаните фигури и таблици можем да обобщим следното, че при трифазно късо съединение през активно съпротивлението в мястото на късо съединение, изчисленията за импеданса не дават точен резултат. Ако се откажем от използването на R и работим само с X, то грешката ще бъде по-малка. Литература 1. И. Л. Небрат, Расчеты токов короткого замыкания для релейной защиты. Учебное пособие, часть первая, Санкт-Петербург, 1996. 2. Кузнецов А.П., В.Ю. Лукоянов, Применение и техническое обслуживание микропроцессорных устройств на электростанциях и в электросетях, Часть 1, Фиксирующие индикаторы для определения мест повреждений на воздушных линиях электропередачи, „НЦ ЭНАС”, Москва, 2001 3. Lyubomirov, S.Y.,S.J. Ovcharov, The Use of the A/D Converter of the Type MAX11040 in Relay Protection, Annual Journal of Electronics, 2010, стр. 39-42, ISSN 1313-1842. 4. Lyubomirov, S.Y., S.J. Ovcharov, Research of an Operating System for the Needs of Relay Protection, Annual Journal of Electronics, 2011, стр. 133-136, ISSN 1313-1842.
Bibliographic link: S.Y. Lyubomirov Research results of impedance of power line in case of three-phase short circuit // Online Electric: Electric power industry. New technologies, 2012.–URL: /articles.php?id=59 (Visit date: 03.03.2026)
|