|
Консультант по электроснабжению
Не нашли нужный онлайн-расчет по электроэнергетике? Свяжитесь с нами!
Бот Яша
Бот Яша подскажет как найти нужный онлайн расчет или базу данных на сайте "Онлайн Электрик".
Написать боту.
К определению граничных значений области прерывистых токов регулируемого электроприводаКаверин В.В., канд. техн. наук, доцентКарагандинский государственный технический университет (Республика Казахстан) Рассмотрены основные направления совершенствования регулируемого электропривода постоянного тока. Разработаны математические модели электропривода в режиме динамического торможения для исследования статических характеристик в области прерывистых токов. Определены в общем виде граничные значения области прерывистых токов для электроприводов средней мощности. Ключевые слова: регулируемый электропривод постоянного тока, динамическое торможение, импульсный преобразователь, прерывистый ток, имитационная модель. Регулируемый четырёхквадрантный электропривод постоянного тока нашел широкое применение в горной промышленности, как в машинах и механизмах, используемых для подземной добычи, так и при открытых горных работах. В странах СНГ налажено серийное производство угледобывающих комбайнов с тиристорным электроприводом механизма подачи. Разработаны экспериментальные и опытные образцы регулируемых электроприводов постоянного тока подземных напочвенных канатных дорог, очистных комбайнов и скребковых конвейеров. Основным оборудованием угольных разрезов являются экскаваторы и буровые станки, оснащённые реверсивным регулируемым электроприводом постоянного тока. В анализируемых классах машин и механизмов используется регулируемый электропривод средней мощности до 100 кВт [1].Появление серийно производимых силовых гибридных транзисторов позволило осуществить разработку импульсных преобразователей повышенной частоты для электроприводов постоянного тока малой и средней мощности. Использование в электроприводе силовых импульсных преобразователей нового поколения не только улучшает его динамические характеристики, но и повышает надёжность привода по сравнению с тиристорными выпрямителями за счёт отсутствия канала синхронизации. Значительное улучшение статических и динамических характеристик придаёт электроприводу применение современных компенсированных электродвигателей средней мощности серии 4ПФ [1]. Один из вариантов схемотехнического решения силовой части четырёхквадрантного электропривода постоянного тока представлен на рисунке 1. 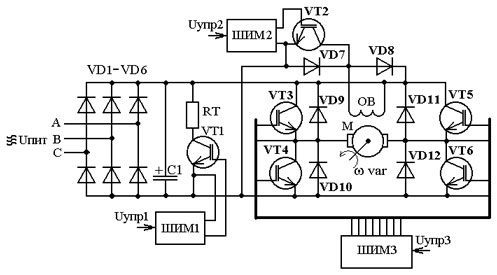 Рис. 1. Схема силовой части четырёхквадрантного электропривода постоянного тока Силовая часть электропривода состоит из неуправляемого выпрямителя VD1-VD6, емкостного сглаживающего фильтра С1 в силовой цепи питания и трёх импульсных преобразователей. Преобразователь выполнен на мостовой схеме VT3-VT6 (ШИМ 3), в диагональ которого включена якорная цепь электродвигателя М, и предназначен для непрерывного управления, как в двигательном, так и в генераторном режимах. Посредством преобразователя VT2 (ШИМ 2) обеспечивается управление током обмотки возбуждения в обоих режимах. С помощью преобразователя VT1 (ШИМ 1) и токоограничивающего резистора RT осуществляется ограничение напряжения на конденсаторе С1 в режиме динамического торможения. Энергия, вырабатываемая электродвигателем в генераторном режиме работы, расходуется на нагрев резистора RT. Переход из двигательного режима в генераторный осуществляется в два этапа. Если в двигательном режиме управление осуществляется посредством транзисторов VT5 и VT4, то для перехода в режим динамического торможения эти транзисторы необходимо закрыть, а транзистор VT3, которым осуществляется шунтирование цепи якоря через диод VD11, перевести в активный режим. Особенностью схемотехнического решения силовой части электропривода (рисунок 1) является то, что электроприводу в генераторном режиме работы не требуется электроэнергия от внешнего источника. Питание системы управления и цепи обмотки возбуждения можно осуществлять энергией конденсатора С1, заряд которого в генераторном режиме осуществляется от ЭДС якоря электродвигателя. Предложенная схема силовой части электропривода позволяет осуществлять непрерывное управление торможением по цепи якоря как в технологическом режиме работы электропривода при наличии электроэнергии, так и в аварийном при несанкционированном её отключении. В процессе имитационных экспериментов установлено, что в режиме динамического торможения в зависимости от скважности импульсного преобразователя VT3-VT6 (ШИМ3), посредством которого осуществляется управление режимом динамического торможения (ИПДТ), ток якоря может быть как прерывистым, так и непрерывным. Прерывистый ток является характерным для электропривода в режиме динамического торможения, выполненного посредством шунтирования цепи якоря импульсным преобразователем. Регулировочные и механические характеристики очень сильно отличаются друг от друга при непрерывном и прерывистом токах соответственно [2]. В связи с этим актуальной задачей является определение граничных значений области прерывистых токов для электроприводов средней мощности. Теоретические исследования электропривода были проведены на базе электродвигателей серии 4ПФ. Механическая постоянная времени даже без учёта маховых масс рабочего органа и трансмиссии значительно превышает постоянную времени якоря электродвигателя. В связи с этим определение граничных значений скважности ИПДТ с точностью, достаточной для инженерных расчётов, можно определить для постоянного значения скорости на интервале времени равного периоду коммутации. С учётом вышеизложенных допущений разработана схема замещения электропривода в режиме динамического торможения, которая представлена на рис. 2. 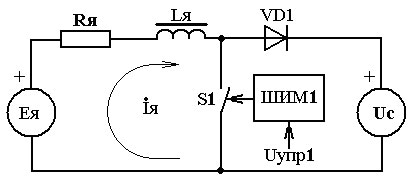 Рис. 2. Схема замещения регулируемого электропривода в режиме динамического торможения Период коммутации импульсного преобразователя состоит из двух временных интервалов, соответствующих замкнутому Δt1 и разомкнутому Δt2 состоянию силового ключа S1. Начальные условия тока якоря в первом интервале Δt1 для прерывистого тока в каждом периоде имеют нулевые значения. Электрические процессы, протекающие в цепи якоря на временных интервалах Δt1 и Δt2 в относительных единицах, описываются следующими дифференциальными уравнениями:
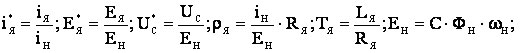 IЯ - ток в цепи якоря; ЕЯ - ЭДС якоря электродвигателя; LЯ, RЯ – суммарные индуктивность и активное сопротивление цепи якоря; С - конструктивная постоянная электродвигателя; UC - напряжение на конденсаторе С1; IН, ЕН, ФН, ωН – номинальные значения тока и ЭДС якоря, магнитного потока и угловой скорости, соответственно. Решением уравнений (1)-(3) с учётом начальных условий (Н.У.) являются зависимости токов якоря в функции времени для замкнутого и разомкнутого состояния ключа, шунтирующего цепь якоря, которые имеют вид:
где t1, t2 – текущее время на интервалах Δt1 и Δt2 соответственно; Δt1 и Δt2 – интервалы времени, соответствующие замкнутому и разомкнутому состоянию ключа S1 (рис. 2); T – период коммутации силового ключа S1 ИПДТ; 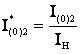 ; ;I(0)2 - начальное значение тока якоря для интервала времени, соответствующего разомкнутому состоянию ключа S1 (рис. 2). Подставляя начальные условия (6) в уравнение (5) получаем зависимость тока якоря в функции времени на интервале Δt2.
Выполняя условия
получаем зависимость граничных значений скважности силового ключа S1 (рис. 2) для прерывистого тока якоря в общем виде:
Величина напряжения U*C и период коммутации ИПДТ (рис. 2), в процессе торможения не изменяются. В связи с этим граничное значение скважности зависит только от численных значений - постоянной времени якорной цепи ТЯ и ЭДС якоря Е*Я. Решить уравнение (8) в общем виде относительно γ затруднительно. С целью дальнейшего исследования области граничных значений скважности, соответствующих переходу электропривода из режима прерывистого в режим непрерывного тока, использован численный метод решения уравнения (8). Решение уравнения реализовано с использованием средств имитационного моделирования в среде MatLab.
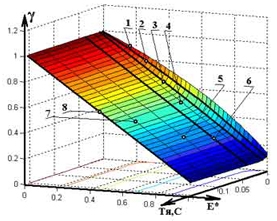
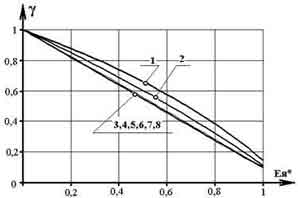
В результате имитационных экспериментов получена графическая зависимость граничного значения скважности в функции постоянной времени ТЯ и ЭДС якоря. Для электродвигателей с ТЯ ≤ 0,1Т (где Т=0,001 с - период коммутации ИПДТ) зависимость граничных значений скважности, соответствующих переходу от прерывистого тока к непрерывному, в функции ЭДС якоря, близка к линейной и практически не зависит от величины постоянной времени ТЯ (рис. 3а) [4]. С целью подтверждения этого вывода в табличном редакторе Microsoft Excel получены проекции величины скважности в функции Е*Я для различных значений ТЯ. Максимальная ошибка между граничными зависимостями скважности для интервала 0,009469 с ≤ ТЯ ≤ 0,1541 с не превышала 1 %.
Переходные процессы тока в цепи якоря электродвигателя описываются уравнениями (4 и 5) с учётом начальных условий (6). Графические зависимости тока якоря для замкнутого (iЯ1) и разомкнутого (iЯ2) состояния ключа S1 (рис.2) представлены на временных интервалах Δt1 и Δt2 соответственно (рис.5). 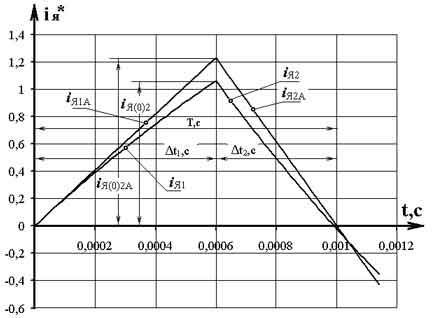 Рис. 5. Переходной процесс тока якоря за полный период коммутации импульсного преобразователя для ТЯ=0,009469 с, Е*Я =0,5 Переходные процессы увеличения (интервал Δt1) и уменьшения (интервал Δt2) тока в цепи якоря электродвигателя описываются экспоненциальными законами — уравнения (4) и (5) соответственно. В том случае, когда ТЯ >> Т, экспоненциальные зависимости тока якоря можно аппроксимировать линейными зависимостями с точностью достаточной для инженерных расчётов. Линейные уравнения можно получить путём разложения в ряд Тейлора уравнений (4) и (5) для соответствующих интервалов времени периода коммутации ИПДТ:
где: iЯ1А, iЯ2А – аппроксимированные зависимости тока якоря в функции времени на интервалах Δt1 и Δt2 соответственно; i(0)2А-начальные условия для второго интервала времени Δt2. На рис. 4 представлены аппроксимированные зависимости iЯ1А и iЯ2А для значений ТЯ = 0,009469 с и Т=0,001 с. Максимальное значение ошибки аппроксимированных зависимостей (9) и (10) относительно зависимостей (4) и (5) соответственно не превышало 5 %. Подставляя аппроксимирующие уравнения (9) и (10) в выражение (8) получаем в общем виде упрощенную форму аналитической зависимости граничных значений скважности для режима прерывистого тока для Тя > 0,009469 с и Т=0,001 с.
Таким образом, для четырёхквадрантного регулируемого электропривода постоянного тока в режиме динамического торможения: - обоснована схема замещения силовой части электропривода постоянного тока в режиме динамического торможения для получения граничных значений прерывистого тока якоря; - определены выходные координаты и коэффициенты регулируемого электропривода влияющие на граничные значения тока якоря электродвигателя; - разработана имитационная модель вычисления граничного значения скважности импульсного преобразователя шунтирующего цепь якоря электродвигателя в режиме динамического торможения; - получена упрощенная форма алгебраической зависимость граничных значений скважности импульсного преобразователя S1-ШИМ1 для условий ТЯ > 0,009469 с и Т=0,001 с; - определён диапазон постоянных времени якорной цепи, для которых ошибка алгебраической зависимости граничных значений области прерывистого тока якоря электродвигателя не превышает 5 %. 1. Каверин В.В. Исследование и разработка управляемых систем динамического торможения регулируемого электропривода постоянного тока горных машин. Автореф. дис. канд. техн. наук. – Алматы, 2001. 20 с. 2. Каверин В.В. Статические характеристики динамического торможения полупроводникового электропривода постоянного тока с импульсным преобразователем.// Труды 1-го международного семинара студентов, аспирантов и учёных «Системный анализ, управление и обработка информации» (27-30 сентября 2010 г.). Ростов-на-Дону, ДонГТУ, 2010. С. 21-28. 3. Брейдо И.В., Эм Г.А. К вопросу об использовании генераторных режимов в тиристорном электроприводе постоянного тока горных машин // Вестник Алматинского института энергетики и связи. 2008. № 3. С. 52-54. 4. Быстродействующие электроприводы постоянного тока с широтно-импульсными преобразователями / М.Е. Гольц, А.Б. Гудзенко, В.М. Остеров и др. – М.: Энергоатомиздат, 1986. 184 с. 5. Черных И.В. Моделирование электротехнических устройств в MATLAB, SimPowerSystems и Simulink. – М.: ДМК Пресс; СПб.: Питер, 2008. 288 с. Библиографическая ссылка на статью: Каверин В.В. К определению граничных значений области прерывистых токов регулируемого электропривода // Онлайн Электрик: Электроэнергетика. Новые технологии, 2012.–URL: /articles.php?id=5 (Дата обращения: 03.03.2026)
|
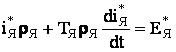 ,
,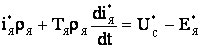 ,
,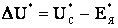 .
.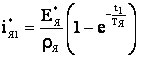 ,
,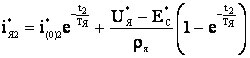 ,
,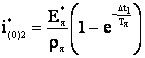 .
.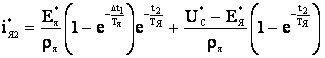 ,
,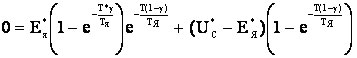 ,
,
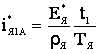 ,
,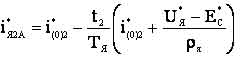 ,
,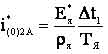 ,
,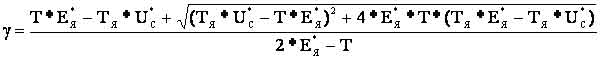 ,
,