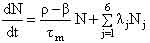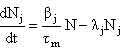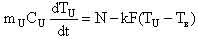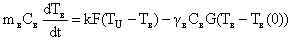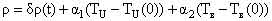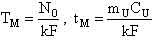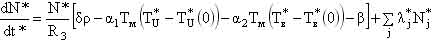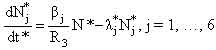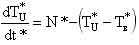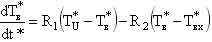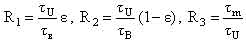|
Консультант по электроснабжению
Не нашли нужный онлайн-расчет по электроэнергетике? Свяжитесь с нами!
Бот Яша
Бот Яша подскажет как найти нужный онлайн расчет или базу данных на сайте "Онлайн Электрик".
Написать боту.
Численные эксперименты по математическому моделированию кинетики ядерного реактораВольман М.А.ФГБОУ ВПО «Ивановский государственный энергетический университет имени В.И. Ленина»
Все естественные и общественные науки, использующие математический аппарат, по сути, занимаются моделированием: заменяют реальный объект его математической моделью и затем изучают последнюю, что позволяет выделить для исследования наиболее важные свойства объекта, абстрагируясь от несущественных его характеристик. Часто удается сформулировать новые гипотезы и получить новые знания об объекте, которые были недоступны, а для сложных объектов появляется возможность избежать слишком больших затрат, необходимых для их непосредственного изучения. Построение модели и формализация связей между ее элементами позволяет устранить пробелы в знаниях об объекте и выявить новые качественные проблемы, которые изначально не могли быть предусмотрены.
Вопросы динамики реактора относятся к наиважнейшим, непосредственно определяющим безопасность его работы. Поэтому им уделяется самое пристальное внимание на стадиях разработки, проектирования, наладки и эксплуатации АЭС, а их изучение является залогом надежной, безопасной и экономичной работы реакторных установок. Сочетание многочисленных достоинств математического моделирования и неоспоримой важности изучения процессов, происходящих в ядерном реакторе, определяет актуальность работы по созданию математической модели кинетики реактора. Кроме того, представляется перспективным ее использование в качестве лабораторного практикума, позволяющего студентам изучить физические процессы, протекающие в реакторе. Цель работы состоит в моделировании процессов разгона и глушения неотравленного реактора с учетом температурных обратных связей и в применении модели для количественного исследования ряда важных для теории и практики нейтронно-физических процессов. В отличие от холодного состояния реактор, находящийся в энергетических режимах (горячий реактор), характеризуется отрицательной обратной связью по температуре топлива и теплоносителя:
Кинетика горячего реактора определяется следующей системой нелинейных дифференциальных уравнений [1]:
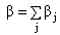 – суммарная доля запаздывающих нейтронов; τm – приведенное время жизни одного поколения мгновенных нейтронов; mU и CU – соответственно масса и удельная теплоемкость топливной загрузки; k, F, TU – соответственно коэффициент теплоотдачи, поверхность теплоотдачи и температура топлива; TВ, TВХ – соответственно температура теплоносителя на выходе и входе в реактор; γ В, CB, – соответственно плотность, удельная теплоемкость теплоносителя при постоянном давлении и расход теплоносителя; δρ(t) – внешнее возмущение реактора по реактивности. – суммарная доля запаздывающих нейтронов; τm – приведенное время жизни одного поколения мгновенных нейтронов; mU и CU – соответственно масса и удельная теплоемкость топливной загрузки; k, F, TU – соответственно коэффициент теплоотдачи, поверхность теплоотдачи и температура топлива; TВ, TВХ – соответственно температура теплоносителя на выходе и входе в реактор; γ В, CB, – соответственно плотность, удельная теплоемкость теплоносителя при постоянном давлении и расход теплоносителя; δρ(t) – внешнее возмущение реактора по реактивности. Начальные условия, без которых эти уравнения не имеют смысла, записываются в виде: при t = 0 N=N0, 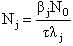 , TU= TU(0), TВХ=const, δρ(0), т.е. в качестве начальных условий задаются мощность реактора, вклад всех групп запаздывающих нейтронов, температуры топлива и теплоносителя, начальный скачок реактивности (начальное внешнее возмущение реактора). , TU= TU(0), TВХ=const, δρ(0), т.е. в качестве начальных условий задаются мощность реактора, вклад всех групп запаздывающих нейтронов, температуры топлива и теплоносителя, начальный скачок реактивности (начальное внешнее возмущение реактора).Реализуемая математическая модель уравнений базируется на следующих допущениях и ограничениях. Во-первых, она записана для реактора с сосредоточенными параметрами («точечный» реактор). Тем самым предполагается, что за время переходного процесса пространственное распределение нейтронного поля реактора не успевает заметно измениться. Во-вторых, также считается, что за время протекания вышеназванных процессов не изменяются концентрация борной кислоты и отравление реактора ксеноном и самарием. Третье ограничение касается гипотезы замыкания приведенной системы уравнений. Дело в том, что реактор через систему трубопроводов связан с системами первого контура, а через парогенератор – с системами второго контура и, кроме того, он находится под управлением автоматики. Так как в настоящем исследовании нас интересует физика процессов, непосредственно протекающих в реакторе, то в качестве гипотезы замыкания исходных уравнений полагаем температуру на входе в реактор постоянной, а автоматику отключенной. Предлагаемая гипотеза замыкания позволяет количественно проанализировать переходные и аварийные режимы в реакторной установке без учета вторичных факторов и действия автоматики, что для понимания физики процессов чрезвычайно важно. Чтобы обнаружить факторы, влияющие на процессы, введем характерные для задачи единицы измерения всех физических величин, или, как принято говорить, безразмерные переменные. В качестве масштаба мощности возьмем установившуюся мощность реактора до начала переходного процесса N0, а масштабы времени tM и температуры TM выберем так, чтобы в уравнении (5) коэффициенты при первом и третьем слагаемом оказались равными единице. Отсюда:
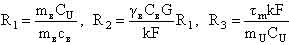 – критерии подобия задачи. – критерии подобия задачи. Численные значения этих критериев удобно выразить через характерные параметры реакторной установки. Для реактора ВВЭР-1000 типичны следующие количественные характеристики: 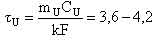 сек – характерное время теплопередачи от топлива к теплоносителю; сек – характерное время теплопередачи от топлива к теплоносителю; 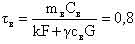 сек – характерное время установления температуры теплоносителя за счёт процессов теплопередачи от топлива к теплоносителю и выноса теплоты в парогенератор; сек – характерное время установления температуры теплоносителя за счёт процессов теплопередачи от топлива к теплоносителю и выноса теплоты в парогенератор; 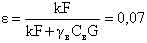 – коэффициент эффективности теплопередающей поверхности. – коэффициент эффективности теплопередающей поверхности. Выражая критерии подобия через приведённые количественные характеристики, получим:
Численные эксперименты на основе реализованной математической модели позволяют количественно исследовать ряд важных для теории и практики нейтронно-физических процессов в ядерном реакторе ВВЭР-1000. Сюда относятся: - исследования устойчивости реактора при малых случайных возмущениях реактивности; - исследования динамики разгона реактора в аварийных режимах с любым наперёд заданным законом роста реактивности реактора во времени; - исследования динамики перехода реактора с одного уровня мощности на другой; - исследования динамики глушения реактора при сбрасывании стержней аварийной защиты с учётом конечного времени падения стержней и соответствующим законом ввода реактивности. Кроме того, подключение к данному блоку подпрограмм, определяющих изменение реактивности реактора вследствие изменения концентрации борной кислоты или отравления реактора ксеноном и самарием, позволит количественно исследовать кинетику реактора при многофакторном изменении его реактивности. Сопоставление результатов расчёта с экспериментами на компьютерной модели на платформе 3KeyMaster позволяет верифицировать отдельные блоки самой компьютерной модели. Приведём один из примеров по реализации данной программы. Он касается исследования устойчивости реактора при его возмущениях по реактивности. Обычно исследования устойчивости разгона реактора, как и исследование устойчивости гидродинамических и других процессов, осуществляется на основе развитой в теоретической физике теории возмущений. Применительно для реактора суть теории заключается в том, что, считая возмущения бесконечно малыми, проводят линеаризацию исходных нелинейных уравнений, пренебрегая бесконечно малыми второго порядка малости. Решения полученных таким способом линейных уравнений для возмущённого движения позволяют выявить характер процессов в реакторе в первые моменты времени после выхода из критического состояния. Недостатком такого подхода является ограниченность предсказания поведения реактора на более поздние моменты времени и невозможность рассмотрения больших возмущений, когда учётом нелинейных эффектов пренебречь нельзя. Предлагаемая выше математическая модель позволяет проследить за динамикой процессов без вышеуказанных ограничений. На графиках (рис. 1) приведены кривые, показывающие характер развития процесса при положительном скачке реактивности δρ=0,005, когда реактор близок к состоянию мгновенной критичности. При разных параметрах топливной загрузки, заложенных в компьютерную модель, возврат реактора в стационарное состояние происходит либо по апериодическому, либо по периодическому процессу. Из сравнения кривых зависимости мощности реактора от времени при одинаковом возмущении по реактивности видно, что при апериодическом процессе выброс нейтронной мощности реактора больше, чем при периодическом процессе. Во втором случае за счёт более сильной отрицательной обратной связи по температуре в ходе затухающего колебательного процесса реактор перейдёт на уровень мощности в 1,05 мощности реактора до начала переходного процесса N0, тогда как при слабой отрицательной обратной связи он перейдёт на более высокий энергетический уровень 1,5N0. Поскольку характеристики различных топливных загрузок реакторов могут весьма значительно отличаться друг от друга (особенно при переходе на новое топливо), то описанные выше особенности в динамике реакторов нужно учитывать в эксплуатации. 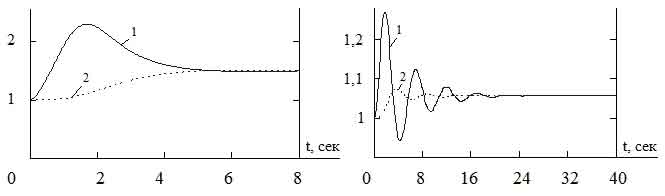
Рис. 1. Зависимость мощности от времени в апериодическом процессе (слева) и в периодическом процессе (справа): 1 – нейтронная мощность, 2 – тепловая мощность. Модель неотравленного реактора с учетом температурных обратных связей позволяет изучить широчайший спектр вопросов, связанных с процессами, происходящими в реакторной установке, дает возможности для понимания физики этих процессов, наглядно показывает важнейшие параметры, влияющие на динамику реактора. Кроме того, подключение соответствующих подпрограмм позволяет количественно исследовать кинетику реактора при многофакторном изменении его реактивности. Применение модели в целях обучения решает вопрос не только изучения конкретной дисциплины, но и создания у студентов начальных навыков моделирования физических процессов. 1. Семенов В.К. Кинетика и регулирование ядерных реакторов. – Иваново, ИГЭУ, 2009. 2. Методики расчета нейтронно-физических характеристик по данным физических экспериментов на энергоблоках атомных электростанций с реакторами ВВЭР-1000 (РД ЭО 0151-2004). – Концерн «Росэнергоатом», 2005. 3. Кирьянов Д.В. Mathcad 13 в подлиннике. – СПб.: БХВ – Петербург, 2005. Библиографическая ссылка на статью: Вольман М.А. Численные эксперименты по математическому моделированию кинетики ядерного реактора // Онлайн Электрик: Электроэнергетика. Новые технологии, 2012.–URL: /articles.php?id=28 (Дата обращения: 11.02.2026)
|