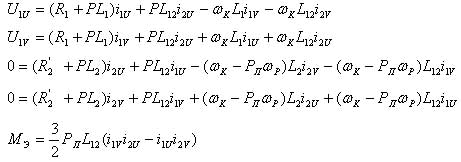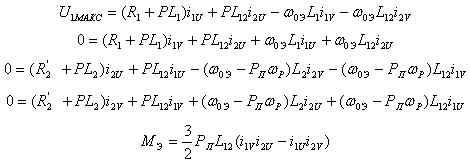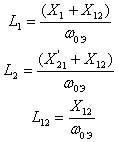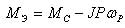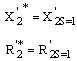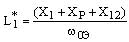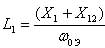Online Electric

     В технологических комплексах промышленных предприятий широко используются механизмы, приводящиеся в движение с помощью нерегулируемых электроприводов. К таким механизмам относятся: насосы различного назначения, вентиляторы и др. К основным особенностям электроприводов указанных механизмов следует отнести:
     - использование в качестве исполнительных двигателей асинхронных двигателей переменного тока с короткозамкнутым ротором;
     - питание в аварийных режимах от автономных источников электрической энергии (дизель-генераторов, газопоршневых генераторов и др.), мощность которых соизмерима с мощностью исполнительных двигателей.
     Наличие этих особенностей ставит перед проектантом электропривода задачу осуществления пуска асинхронного двигателя, при котором активная мощность, потребляемая им из сети, не превысит критического для первичного двигателя автономного источника электрической энергии значения.
     В современных нерегулируемых электроприводах общепромышленного назначения для решения этой задачи широко используются два технических решения:
     - пуск с помощью полупроводниковых регуляторов напряжения, подводимого к обмоткам статора двигателя;
     - реакторный пуск, при котором исполнительный двигатель подключается к сети через токоограничивающий электромагнитный реактор.
     При использовании полупроводниковых регуляторов напряжения возникает проблема электромагнитной совместимости электропривода с другими потребителями электроэнергии. Решение этой проблемы, в случае соизмеримости мощности электропривода и источника электрической энергии, зачастую встречает непреодолимые трудности. Этого недостатка лишены электроприводы, реализующие реакторный пуск исполнительного двигателя. В связи с этим можно заключить, что в электроэнергетических установках, для которых электромагнитная совместимость потребителей является важнейшим требованием, рациональней использовать электроприводы с реакторным пуском.
     В технической литературе [1], [2] достаточно подробно изложены методики расчета и определения параметров пусковых электромагнитных реакторов. При этом основным критерием, используемым при расчете, является величина пускового тока исполнительного двигателя. Однако при пуске двигателя от источника электрической энергии соизмеримой мощности главным критерием, влияющим на выбор реактора, является не величина потребляемого при пуске тока, а активная составляющая мощности на валу первичного двигателя автономного источника (дизель, газопоршневая машина). К сожалению, в настоящее время отсутствуют методики, учитывающие это обстоятельство, и которые можно было бы использовать для корректного расчета пусковых реакторов, входящих в состав электроприводов указанных выше механизмов.
     В настоящей статье приводится математическая модель электропривода с реакторным пуском, которая позволяет решить эту задачу, используя современные компьютерные технологии. В статье также приводятся основные результаты, полученные в ходе изготовления комплектного пускового устройства для сетевых насосов, входящих в состав технологического оборудования городской котельной. При разработке комплектного пускового устройства была использована методика расчета параметров пускового реактора, в основу которой была положена вышеуказанная математическая модель.
     Основным элементом рассматриваемого класса электроприводов является асинхронный двигатель с короткозамкнутым ротором. Процесс электромеханического преобразования энергии в нем описывается системой уравнений Парка – Горева, которые, будучи записанными в системе координат U, V, вращающихся с произвольной угловой скоростью ω_K, имеют вид [3]

.

(1)

Здесь в системе уравнений (1)
      U_1U, U_1V -проекции вектора фазного напряжения, прикладываемого к обмоткам статора двигателя, на координатные оси U, V, В;
      i_1U, i_1V, i_2U, i_2V - проекции векторов фазных токов, протекающих в обмотках статора и ротора, на координатные оси U, V, А;
      R₁, R’₂ - активные сопротивления фазных обмоток статора и ротора, Ом;
      L₁, L₂ - собственные индуктивности фазных обмоток статора и ротора, Гн;
      L₁₂ - взаимная индуктивность между фазными обмотками статора и ротора, Гн;
     P=d/dt -оператор Лапласа;
      M_Э -электромагнитный момент на валу двигателя, Нм;
      P_П -число пар полюсов двигателя;
      ω_Р -угловая скорость вращения ротора двигателя, 1/с.
     Если угловую скорость вращения системы координат ω_K принять равной угловой скорости вращения магнитного поля ω_0Э=2πf₁ (f₁-частота напряжения, прикладываемого к обмоткам статора) и расположить оси координат таким образом, чтобы ось U совпадала с обобщенным вектором напряжения статора, то уравнения, описывающие процесс электромеханического преобразования энергии, протекающий в асинхронном двигателе, будут иметь следующий вид

,

(3)

где U_1МАКС -амплитудное значение фазного напряжения электрической сети В.      Величины собственных индуктивностейL₁, L₂, а также взаимной индуктивности L₁₂ могут быть определены по формулам [3]

,

(4)

здесь X₁, X’₂ и X₁₂ индуктивные сопротивления обмоток статора и ротора, а также индуктивное сопротивление контура намагничивания. Численные значения этих сопротивлений указываются в паспортных данных двигателей.
     Для описания электромеханических процессов, протекающих в электроприводе при реакторном пуске двигателя, нужно систему уравнений (3) дополнить уравнением механического равновесия моментов на валу двигателя

,

(5)

здесь M_C -статический момент нагрузки, приведенный к валу двигателя, Нм;       J -момент инерции, приведенный к валу двигателя, км².
     Аналитическое совместное решение системы дифференциальных уравнений (3) и уравнения (5) представляет собой непреодолимые трудности. Поэтому для исследования электромеханического процесса, протекающего в электроприводе при реакторном пуске, необходимо пользоваться средствами вычислительной техники, в частности, используя пакет прикладных компьютерных программ MATLAB. В обеспечение последнего нужно разработать компьютерную модель электропривода, соответствующую системе уравнений (3) и (4). Схема такой модели показана на рис.1.
     При разработке модели было учтено, что индуктивное сопротивление обмотки статора, а следовательно и величина L₂ в процессе разгона двигателя изменяют свои значения. Изменяет свое значение и активное сопротивление ротора R’₂. Как показано в [4] с достаточной степенью точности можно принять, что на интервале скольжений 1≤S≤S_КР индуктивное сопротивление фазы ротора X’₂ и активное сопротивление фазы ротора R’₂ остаются величинами постоянными и равными

,

(6)

где X’_2S=1 и R’_2S=1 - индуктивное и активное сопротивление фазы ротора при скольжении равном 1 (двигатель находится в заторможенном состоянии). Численные значения этих параметров обычно в паспортных данных двигателя не приводятся, но они могут быть получены от предприятия - изготовителя по соответствующему запросу. На интервале S_КР≤S≤S_Н индуктивное сопротивление фазы ротора X’₂ и активное сопротивление фазы ротора R’₂ также остаются величинами постоянными, но уже равными значениям, указанным в паспортных данных.
     Поскольку при реакторном пуске асинхронного двигателя последовательно его статорным обмоткам включается трехфазный реактор, обладающий индуктивным сопротивлением X_P, то величина собственной индуктивности статора L₁ также претерпевает изменение. То есть при включенном реакторе величина собственной индуктивности равна

,

(7)

и соответственно при зашунтированном реакторе

.

(8)

     Из рис.1 следует, что разработанная компьютерная модель электропривода с реакторным пуском асинхронного двигателя представляет ой совокупность библиотечных блоков пакета MATLAB (блоки постоянных величин, блоки усиления, блоки апериодических звеньев, блоки умножения, блоки деления, блоки суммирования). Некоторые из используемых блоков в процессе разгона двигателя изменяют свою передаточную функцию (в моделе эти изменения осуществляются с помощью управляемых ключей ключей S1-S14).
     Выходными координатами модели являются частота вращения ротора ω_P, а также активная составляющая мощности на валу первичного двигателя источника электрической энергии. Для получения активной мощности в модель вводится блок, обеспечивающий перемножение действующего значения фазного напряжения статора на действующее значение активной составляющей фазного тока статора, а также на величину обратно пропорциональную коэффициенту полезного действия синхронного генератора, который приводит в движение первичный двигатель. Активная составляющая фазного тока статора при принятом расположении координатных осей U, V является проекцией вектора тока статора на ось U (i_1U).
     Входными координатами модели являются амплитудное значение фазного напряжения электрической сети U_1МАКС и угловая скорость вращения магнитного поля двигателя ω_0Э=2πf₁. В случае питания электропривода от сети бесконечной мощности эти координаты имеют постоянные значения. При питании электропривода от источника электрической энергии соизмеримой мощности входные координаты модели тоже были приняты постоянными величинами. Это допущение является корректным, в случае, если дизель- генераторная установка снабжена системой автоматического поддержания их на постоянном уровне при работе на рабочем участке механической характеристики первичного двигателя.
     Компьютерная модель была использована в ходе разработки и изготовления поставочного образца комплектного пускового устройства КПУ-630-УХЛ4. Это устройство предназначалось для работы в составе технологического оборудования городской котельной станции. Комплектное устройство обеспечивало последовательный реакторный пуск трех асинхронных двигателей типа А4-400У-4У3, приводящих в движение сетевые насосы системы гидравлики. Двигатели имели следующие номинальные параметры:
     - мощность - 630 кВт;
     - действующее значение напряжения - 6000В;
     - частота вращения - 1500 об/мин.
     В качестве источника электрической энергии в аварийных режимах эксплуатации сетевых насосов использовалась газо-поршневая установка полной электрической мощностью 3000 кВА. Главной трудностью создания пусковой установки было одновременное выполнение двух требований:
     - обеспечение достаточно большого пускового момента исполнительных двигателей;
     - ограничение активной мощности на валу первичного двигателя газо-поршневой установки при пуске на уровне, не превышающем номинального значения.
     Выполнение этих противоречащих друг другу требований ставило перед проектантом разрабатываемого пускового устройства задачу определения оптимального значения индуктивности пускового реактора. Для решения этой задачи и была использована компьютерная модель реакторного пуска, рассмотренная выше.
     Принципиальная схема силовых цепей пусковой установки КПУ-630-УХЛ4 приведена на рис.2. Работа пускового устройства осуществляется следующим образом. При включении двигателя М1 одновременно включаются сетевые вакуумные выключатели QF1, QF2. При этом обмотки статора двигателя М1 через реактор L1 подключаются к сети.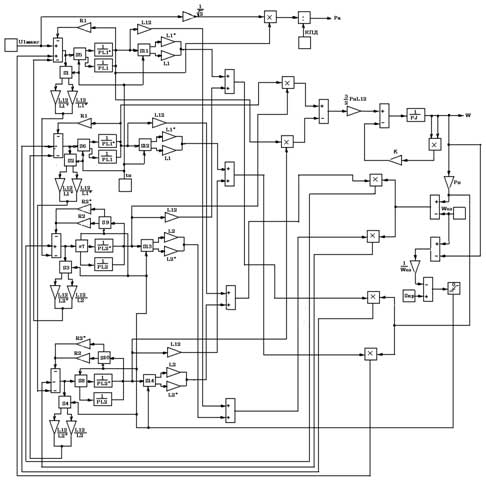



Рис.1. Компьютерная модель электропривода с реакторным пуском переменного тока 6кВ.

     По мере разгона двигателя и снижения потребляемого из сети тока сетевые выключатели QF1, QF2 выключаются, а сетевой выключатель QF3 включается. В результате этого двигатель подключается к сети напрямую и начинает работать на естественной механической характеристике.
     Включение двух остальных двигателей М1, М2 осуществляется аналогично посредством сетевых выключателей QF4-QF7.
     Конструктивно пусковое устройство состояло из реакторного шкафа и трех высоковольтных камер одностороннего обслуживания КСО1-КСО3. В реакторном шкафе размещался пусковой реактор индуктивностью 50 мГн и микропроцессорная система управления, обеспечивающая последовательные пуск и выключение трех асинхронных двигателей либо с дистанционного поста управления, либо с панели местного управления. Система микропроцессорного управления позволяла осуществлять пуск либо в функции потребляемого тока, либо в функции времени. Кроме того, микропроцессорная система управления обеспечивала защиту двигателей от перегрузки и от затянувшегося пуска, а также производила работу световой индикации.
     В камерах одностороннего обслуживания размещались сетевые вакуумные выключатели QF2-QF7 и цепи оперативного управления их работой.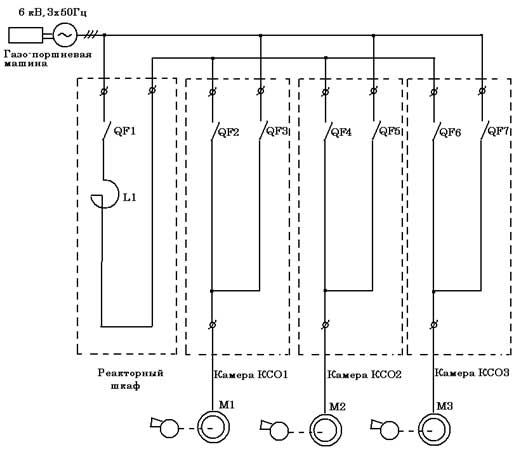



Рис.2. Принципиальная схема силовых цепей пускового устройства типа КПУ-630-УХЛ4

     Шкафы комплектного устройства обладали степенью защиты IP24 и имели следующие массо-габаритные характеристики.

Характеристика	Шкаф реакторный	Камера одностороннего обслуживания
Длина, мм	1000	1000
Высота, мм	2900	2900
Глубина, мм	1495	1495
Масса, кг	1500	100

БИБЛИОГРАФИЧЕСКИЙ СПИСОК
     1. Андреев В.П., Сабинин Ю.А. Основы электропривода. Л.-М.: Госэнергоиздат,1963. 772 с.
     2. Чиликин М.Г. Общий курс электропривода. М.: Энергия, 1971. 576 с.
     3. Чиликин М.Г., Ключев В.И., Сандлер А.С. Теория автоматизированного электропривода. М.:Энергия, 1979. 616 с.
     4. Гревнин Г.Р., Лазаревский Н.А. Реакторный пуск асинхронных двигателей. Л.: Судостроение, 1975. 192 с.