|
Консультант по электроснабжению
Не нашли нужный онлайн-расчет по электроэнергетике? Свяжитесь с нами!
Бот Яша
Бот Яша подскажет как найти нужный онлайн расчет или базу данных на сайте "Онлайн Электрик".
Написать боту.
Indication of flux linkage components used in variable speed drives with vector control.Алексеев В.В., Вершинин В.И.Санкт-Петербургский государственный горный университет
Характерное для мирового уровня внедрение электроприводов переменного тока для манипуляторов, вращателей буровых станков и другого технологического оборудования стало возможным благодаря системам, способным полностью реализовать динамические возможности асинхронной машины. К таким системам относятся системы векторного управления [1, 2]. Анализ литературы показывает, что в современных технологических комплексах, используемых в различных отраслях, в том числе и в горной отрасли, автоматизированные частотно-регулируемые асинхронные электроприводы с алгоритмом векторного управления находят широкое применение [1-3]. Это обстоятельство объясняется двумя причинами, а именно:
- в качестве исполнительных двигателей в таких электроприводах используются надежные, дешевые, не требующие постоянного технического обслуживания, асинхронные двигатели с короткозамкнутым ротором; - по своим динамическим свойствам частотно-регулируемые электроприводы с векторным управлением не уступают электроприводам постоянного тока. Частотно-регулируемые электроприводы с векторным управлением основаны на автономном управлении составляющими обобщенного вектора тока относительно опорного вектора, в качестве которого обычно выступает либо обобщенный вектор главного потокосцепления машины Ψ0, либо вектор потокосцепления ротора Ψr. При синтезе частотно-регулируемых электроприводов с векторным управлением применяются два способа определения параметров векторов потокосцепления: прямой и косвенный. При прямом способе в расточку статора исполнительного двигателя устанавливается датчики Холла. Они позволяют осуществить точную фиксацию составляющих вектора главного потокосцепления Ψ0 относительно неподвижной системы координат статора α, β. Сигналы датчиков соответствуют значению основного магнитного потока в данный момент в месте установки датчиков, а обобщенный вектор потокосцепления ротора оценивается в соответствии с выражением [1] 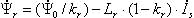 , (1) , (1)где kr – коэффициент потокосцепления ротора; Lr –индуктивность рассеяния ротора. При косвенном определении параметров потокосцеплений пользуются исключительно расчетными методами, в основе которых лежит система дифференциальных уравнений Парка-Горева, которые широко используются при исследовании переходных процессов в асинхронных электрических машинах [1, 4] 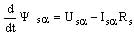 , (2) , (2)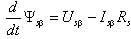 , (3) , (3)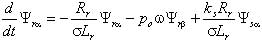 , (4) , (4)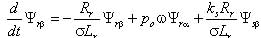 , (5) , (5)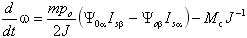 , (6) , (6)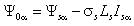 , (7) , (7)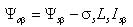 , (8) , (8)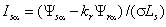 , (9) , (9)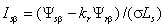 , (10) , (10)Здесь: Is, Ψ0, Ψs, Ψr, Us – проекции обобщенного вектора тока статора, главного потокосцепления, потокосцепления статора и ротора, напряжения статора на оси α–β; Rs, Rr – активные сопротивления статора и ротора, σs = 1 – ks – коэффициент рассеяния статора, σ= 1 – kskr – коэффициент полного рассеяния, ks = Lm/Ls – коэффициент потокосцепления статора, kr = Lm/Lr – коэффициент потокосцепления ротора; Ls – индуктивность статора; Lm – взаимная индуктивность между обмотками статора и ротора; σLs = Ls’ и σLr = Lr’ – переходные индуктивности статора и ротора; m и po – число фаз статора и число пар полюсов; ω – частота вращения ротора; J – момент инерции; Mc – статический момент нагрузки. Другие электромагнитные переменные могут быть определены по формулам [1]
Уравнение, полученное на основании (1, 2) и (7, 8) 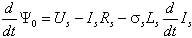 (12) (12)может служить для определения вектора главного потокосцепления, так как интегрирование правой его части обеспечивает его оценку 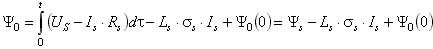 . (13) . (13)Формулам (2-11) соответствуем математическая модель асинхронного двигателя рис.1, используемая при моделировании в компьютерной программе MATLAB (Simulink) 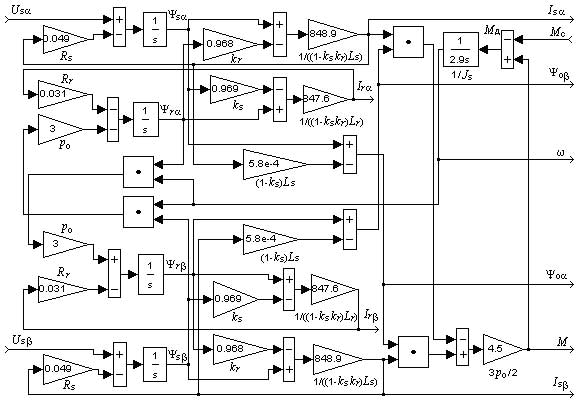 Рис.1. Модель асинхронного двигателя (4A280S6) В настоящей статье приводятся сравнительные результаты определения параметров вектора главного потокосцепления, полученные обоими методами. Эти результаты получены экспериментальным путем при исследовании макетного образца частотно-регулируемого электропривода вентиляторной установки. Перед проведением эксперимента в расточку статора исполнительного двигателя для непосредственного измерения вектора главного потокосцепления были установлены датчики Холла типа ДКХ-7А. Для косвенного измерения использовалась система управления, программный продукт которой реализовывал структурную схему, собранную из библиотечных блоков пакета прикладных программ MATLAB рис.2, (см. рис.1). 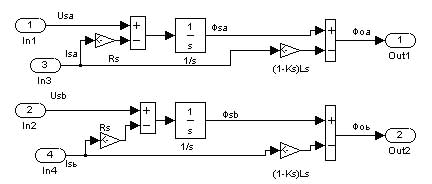 Рис.2. Структурная схема, соответствующая алгоритму управления В качестве датчиков текущих значений тока и напряжения применялись стандартные трансформаторы тока и напряжения: ТК-40-50/5 (ГОСТ 7146-78); T3I3 (ОЛГ.140.083.ТО), установленные в статическом преобразователе частоты. Они включались таким образом, чтобы обеспечить эксплицитность графиков Ψоα(t). Измеряемые с помощью датчика Холла ΨоαДХ и вычислителя Ψ оαВП сигналы составляющей вектора главного потокосцепления, наряду с другими сигналами, подавались на монитор. На рис.3 изображены диаграммы изменения координат электропривода в процессе пуска и разгона исполнительного двигателя до номинальной частоты вращения. Пуск и разгон осуществлялись при векторном управлении с использованием опорного вектора главного потокосцепления, определяемого с помощью датчиков Холла. 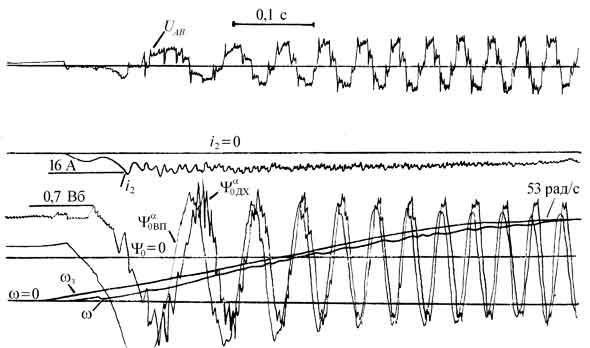 Рис.3. Диаграммы изменения координат электропривода при пуске и разгоне исполнительного двигателя Здесь на приведенных диаграммах представлены: ω3 – сигнал задания частоты вращения исполнительного двигателя; ω – фактическое значение частоты вращения; UAB- линейное напряжение на выходе статического преобразователя частоты; Ψ оαДХ – проекция вектора главного вектора потокосцепления на ось α, измеренная прямым методом с помощью датчика Холла; Ψ оαВП – проекция вектора главного вектора потокосцепления на ось α, определенная косвенным методом. Сравнительный анализ результатов определения параметров вектора главного потокосцепления показывает, что при низких частотах напряжения и тока статора исполнительного двигателя наблюдаются расхождения параметров вектора, полученных прямым и косвенным методом. То есть ошибка при использовании косвенного метода достигает величины 10-15%. Причина этого заключается в том, что в процессе эксперимента использовались трансформаторные датчики тока и напряжения, которые при малых частотах имеют большую погрешность. При непосредственном методе существенную роль играет точность датчиков Холла. Наиболее существенным является параметр температурного дрейфа ЭДС датчика в широком диапазоне температур. Для датчиков типа ДХК-7 в диапазоне изменения температур Дт = 100° C типичным является температурный коэффициент 0,35 %/° C. В широком диапазоне температур ТКЕ нелинейно зависит от температуры. Наиболее критичным является возможное наличие в относительной погрешности аддитивной составляющей. В этих случаях применяют алгоритмы векторной фильтрации. Технологические трудности обеспечения ортогональности составляющих векторов Ψ оαДХ, Ψ оβДХ парируются с помощью алгоритма фазовых преобразований. При исследовании макетного образца частотно-регулируемого электропривода в диапазоне температур от +12 °C до +28 °C влияние изменения ЭДС Датчиков Холла на динамику процессов не отмечено. При косвенном методе, для получения высоких показателей регулирования в широком диапазоне управления скоростью машины переменного тока, необходимо для вычислителя составляющих обобщенного вектора главного потокосцепления применять высокоточные датчики мгновенных значений напряжений и токов, например, датчики производства швейцарской фирмы LEM, которые имеют погрешность во всем диапазоне измеряемых частот не более 1-2 %. Следует отметить, что точность косвенных вычислений зависит от вида опорного вектора системы. Кроме требования высокой точности датчиков мгновенных значений напряжения и тока, следует учитывать наличие в расчетных уравнениях Парка–Горева параметров исполнительного двигателя (Rr, Ls, Lm, Lr). Эти параметры, как известно, определяются режимом работы двигателя. Например, изменение сопротивления алюминиевой клетки ротора в диапазоне температур от +20 °C до +100 °C составляет около 40%. Если не учитывать изменения параметров при косвенном измерении составляющих векторов потокосцеплений, то ошибка в ориентации вращающейся системы координат по направлению вектора потокосцепления может быть значительной (более 5%). Это вызовет значительное снижение качества регулирования системы и потерю преимуществ векторного управления [1]. Температурные изменения сопротивлений медных обмоток ротора и статора меньше, однако, и температурный коэффициент сопротивления меди αt=0,0039 K-1 также вызывает в диапазоне рабочих температур машины изменение сопротивления обмоток, измеряемое десятками процентов. Для компенсации изменения сопротивления в векторных системах используются уравнения, не содержащие сопротивления в явном виде [2, 5]. Но следует иметь в виду, что применяемые в этих уравнениях индуктивности также не постоянны, а являются отражением условий существования магнитного поля [6]. Если учесть изменение параметров, входящих в уравнения (1-13), используемые при вычислениях потокосцеплений, то частотно–регулируемые электроприводы с косвенным и прямым способами определения составляющих вектора главного потокосцепления будут вполне конкурентоспособными. А с учетом такого критерия как надежная работа при воздействии возмущающих факторов (одиночные удары, вибрации), который является наиболее важным фактором при синтезе ряда автоматизированных электроприводов, косвенный способ может быть более предпочтительным. 1. Рудаков В.В., Столяров И.М., Дартау В.А. Асинхронные электроприводы с векторным управлением. Л.: Энергоатомиздат. 1987. 136 с. 2. Алексеев В.В., Дартау В.А. Идентификация электромагнитных переменных в машинах переменного тока: Межвузовский сборник Высокомоментные синхронные двигатели: теория расчет, управление. Новосибирск, изд. НЭТИ, 1989, С. 58-63. 3. Алексеев В.В., Вершинин В.И Сравнительные характеристики систем управления электроприводов для буровых установок.. «Электрофорум», № 6, 2003, С. 37-38. 4. Алексеев В.В., Загривный Э.А., Козярук А.Е. Электрические машины. Моделирование электрических машин приводов горного оборудования. СПб. СПГГИ., 2006, 58 с. 5. Козярук А.Е. Рудаков В.В. Современное и перспективное алгоритмическое обеспечение частотно-регулируемых электроприводов. СПб.: СПЭК. 2004. 127 с. 6. Копылов И.П. Математическое моделирование электрических машин. М. Энергоиздат. 1994. 318 с. Bibliographic link: Алексеев В.В., Вершинин В.И. Indication of flux linkage components used in variable speed drives with vector control. // Online Electric: Electric power industry. New technologies, 2012.–URL: /articles.php?id=15 (Visit date: 11.02.2026)
|