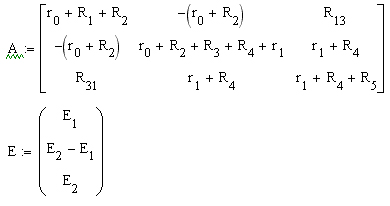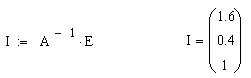Online Electric

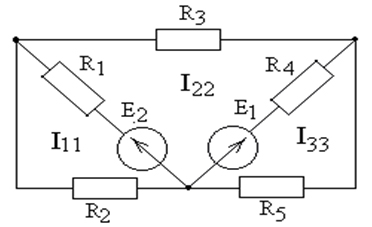
Компьютерное моделирование, проведение вычислительного эксперимента является одним из современных методов исследования электротехнических явлений. Это моделирование основано аналогии между уравнениями, описывающими процессы физической природы. Современный персональный компьютер позволяет за несколько секунд решить сложную систему уравнений, построить график изучаемой зависимости, промоделировать трудновоспроизводимый эксперимент.

Совершенно очевидно, что студенты высших учебных заведений должны иметь представления о компьютерных моделях, численных методах изучения различных объектов познания, достаточно свободно ориентироваться в современных программных продуктах. Для решения задач по предмету “Основы электротехники” от студентов требуется овладения методами вычислительной математики и физики.

С другой стороны необходимо уметь работать с современными математическими пакетами, различными системами компьютерной математики. Таким системам относится MathCAD, Maple, Mathematica и много других систем.

Рассмотрим применение систему MathCAD для решения задач по предмету “Основы электротехники” на решения следующей задачи.

Задача: Цепь состоит из нескольких ветвей, в каждой из которых находится источник ЭДС и резистор (рис.1)[1]. Необходимо рассчитать цепь, то есть определить токи и напряжения во всех ее ветвях.

Дано: E₁=20 В, E₂=24 В, R_e1=2 Ом, R_e2=3 Ом, R₁=5 Ом, R₂=8 Ом, R₃=5 Ом, R₄=7 Ом, R₅=10 Ом. Схему разделим на самостоятельные контуры и направления тока контуров выбираем произвольно (Рис.1).

Общий вид составленного уравнение каждому контуру имеет следующему виду [2]:

(r₀+R₁+R₂)·I₁₁+-(r₀+R₂) ·I₂₂+R₁₃·I₃₃=E₁

(-r₀+R₂)·I₁₁+(r₀+R₂+R₃+R₄+r₁) ·I₂₂+(r₁+R₄) ·I₃₃=E₂-E₁

R₃₁·I₁₁+(r₁+R₄) ·I₂₂+(r₁+R₄+R₅) ·I₃₃=E₂

Здесь r₀=R_В1 и r₁=R_В2; R₁₃=0; R₃₁=0.

Этого уравнение записываем матричном виде:

AI=E.

Здесь

A^-1 обратная матрица на A.

Определяем токов контуре:

I₀=1.6; I₁=0.4; I₂=1;

J₁=I₀; J₂=I₀-I₁; J₃=J₁; J₄=I₂+I₁; J₅=I₂;

J₁=1.6; J₂=1.2.

Определяем падения напряжений в цепи:

U₁=J₁R₁; U₁=8;

U₂=J₂(R₂+r₀); U₂=12;

U₃=J₃R₃; U₃=2;

U₄=J₄(R₄+r₁); U₄=14;

U₅=J₅R₅; U₅=10.

Решение проверим по второму закону Кирхгофа:

E₁=U₁+U₂; E₁=20;

E₂=U₄+U₅; E₂=24; E₂-E₁=4.

Проверим баланс активных и реактивных мощностей. Мощность источника тока S_ИСТОЧ должна быть равна суммарной мощности приемников тока S_ПРИЕМ.

ΣS_ИСТОЧ= ΣS_ПРИЕМ

E₁·J₁+E₂·J₂=60.8l;

(J₁)²·(R₁+r₁)+(J₂)²·R₂+(J₃)²·R₃+(J₄)²·(R₄+r₀)+(J₅)²·R₅=60.44.

Внедрение в учебный процесс компьютерной техники позволяет существенным образом изменить методику изучения некоторых вопросов курса электроэнергетики, связанных с осуществлением громоздких, многократно повторяющихся вычислительных процедур, решением систем уравнений, построением графиков и поверхностей, наглядным представлением результатов решения задачи.

1. В.А. Прянишников. «Электротехника и ТОЭ» в примерах и задачах. Санкт-Петербург, «Корона», 2001 г.

2. Е.Р.Алексеев, О.В. Чеснокова «Решение задач вычислительной математики в пакетах MATCAD 12, MATLAB 7, MAPLE 9», НТ Пресс, 2006, (самоучитель)